DC Filament Supply Test

ClariSonus Research Report #002

by John Atwood
March 14, 2007
(updated March 23, 2007)

This report is licensed by the Creative Commons Attribution-NoDerivs 2.5 license.

Introduction

After discussions with Lynn Olson on the merits of different designs for filament supplies, I decided to compare various design topologies and take some measurements. These measurements and waveforms are referenced in Lynn's posting on the ClariSonus blog.

A representative filament load was chosen: 5.0V at 2.5A. This is roughly equivalent to two 300Bs in parallel or one "super" 300B. To avoid blowing out tubes, a 2.0 ohm 20W power resistor was substituted as the load. A large C-core transformer with a "9.5V" at 4.5A winding was chosen. The primary is rated at 115V. It has another 24V, 5.5A winding that was unused. When powered from a 120V line, the output is about 10V. The filter capacitors are Panasonic type ECO-S1VA103CA 105°C types. The bridge rectifier is an old (1970) Motorola epoxy-encased 12A, 50V type. The capacitor charging current is measured by a 4-wire power resistor with an experimentally-determined resistance of 6 milliohms. Since this circuit exists only for this report, no effort was made to put it on a chassis, so it is "air-insulated" as this picture of circuit #1 shows:

Filament Test Circui

Various topologies were tried that, where possible, used the same components. A problem is that these different topologies give different output voltages. In order to simulate the same tube filament load, either the input voltage could be changed, say by a Variac, or the voltage could be dropped by a power resistor right before the load. Since I didn't want to insert any extra impedances between the power line and rectifier, the latter was chosen. A large 7.5 ohm rheostat was used to drop the voltage to 5.0V. The resistance setting of the rheostat is listed in each schematic.

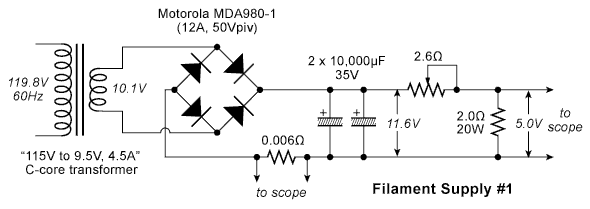
Circuit #1 - Simple Cap-Input

Circuit number one is a simple capacitor-input supply seen in nearly every DC filament supply, as well as virtually all solid-state amplifiers. It has the merit of simplicity, but several disadvantages electrically. Here is the circuit: Circuit #1 schematic

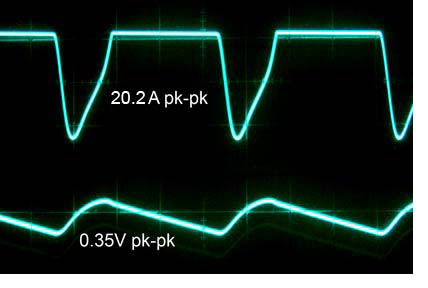
One of the biggest problem with this topology is that current is drawn from the line in short bursts at the top of each cycle. The larger the capacitors and the lower the impedance between the power line and the capacitor, the bigger the charging pulses. These pulses have high harmonic content, and if there is any open loop area where this current flows, a magnetic field is generated which will inject this noisy signal into signal loops. Also, if the signal ground is carelessly connected to the wrong place, such as right at the rectifier terminal, then voltage drops in the wiring will inject these pulses into the ground system. The sound of both of these problems is a characteristic "buzz" at twice the line frequency.

Another problem is that the ripple voltage is not sinusoidal, but rather somewhat like a sawtooth wave, again with high harmonic content. Here are the waveforms and peak-to-peak values of the charging current and output ripple:

Circuit #1 waveforms

The width and amplitude of the charging pulse are, frankly, less than I would have expected. On further examination, I found that the waveform at my house was pretty lousy, with flat-tops that would extend the charging times. Here is the waveform, as measured at a wall-socket in a circuit with no other loads, so is representative of what is present on my main circuit-breaker panel:

House waveform

Circuit #2 - Cap-Input with Resistance Ahead of Capacitor

Instead of dropping more than half the DC voltage in the rheostat, what about putting the resistance ahead of the capacitors? The rheostat was moved over and readjusted to give 5.0V output:

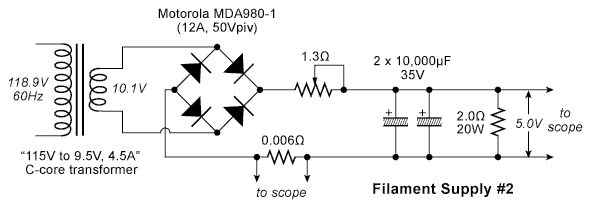
Note that the rheostat is now at about half the previous value. This is because voltage is only dropped during the narrow, but large charging pulses, so less resistance is needed. The charging pulses are less than half as big and are spread out to about 2/3rds of a cycle (a cycle here being 1/120th of a second). The ripple voltage is a little higher, but now nearly sinusoidal:

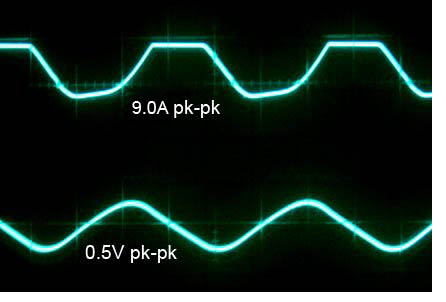
Circuit #2 waveforms

Circuit #3 - Resistance Between Two Capacitors

What happens when we use a two-stage filter, in other words a cap-input charging capacitor follower by an R-C filter section? By putting the rheostat between the two 10,000µF capacitors, this can be done without increasing the amount of parts in the circuit. As expected, the rheostat value is close to the value in circuit #1, since it is dropping mostly DC voltage. Here is the circuit:

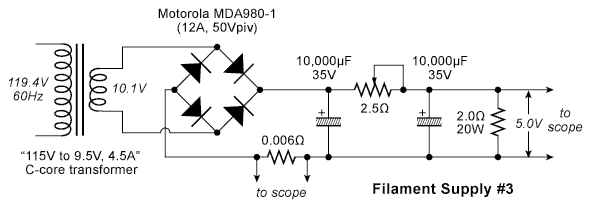
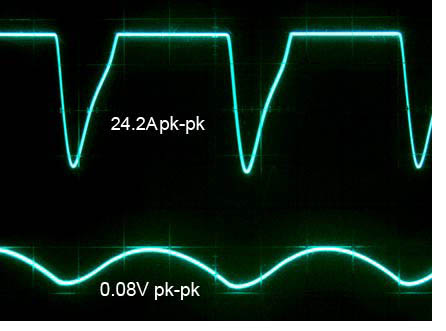
This circuit configuration produced two surprises: the good one is that the ripple is very low, but the bad one is that the charging current is higher than in circuit #1. The low ripple shows the benefit of having an actual filter capacitor in the circuit. (Note that I have been not been calling the input capacitor a "filter" capacitor, but rather a "charging" capacitor, which is really its actual function. This is case where semantics affect people's understanding of the physical world - by calling the first capacitor a "filter" capacitor, they think that by making it bigger, it will filter better. It often doesn't.) I'm not sure why the charging pulses are higher - they should be lower, due to the lower input charging capacitor. Maybe the R-C network following it sets it up to charge faster. SPICE simulation might help here.

Circuit #3 waveforms

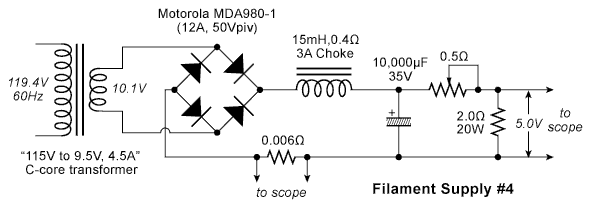
Circuit #4 - Choke Input

In the final circuit, one of the 10,000µF capacitors is replaced by a choke. This is not a cost-constant trade, since the choke is much larger, heavier, and more expensive than the capacitor. Here is a size comparison:

Choke vs Capacitor

The choke is a hand-wound prototype used for the Artemis Labs SP-1 amplifier, where it is used in a choke input supply for a "super" 300B filament.

This time, there was little excess voltage from the supply, so the rheostat was almost at zero ohms:

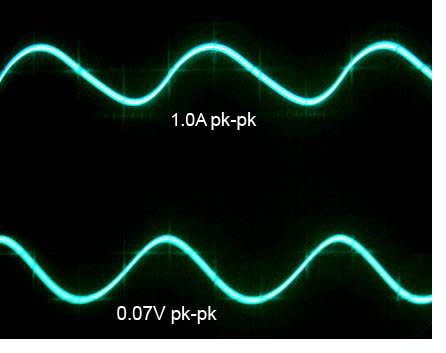
Several notable things here: the ripple is very low and almost sinusoidal, and the "charging" current is very low - a 1.0A near sine wave. At first I was a little confused, because this AC current I measured was significantly less than the AC current drawn from the transformer. Then I realized that this is the "ripple" current. If I moved the 0.006 ohm sense resistor to the AC side of the bridge, I would see the actual line current waveform. The larger the choke inductance, the lower this ripple current will be, and also the lower the output voltage ripple.

Circuit #4 waveforms

Ripple and Charging Spectrum

To show the difference between the topologies in frequency spectrum, circuits #1 and #4 were analyzed by my Audio Precision System 2. All the following plots are just showing relative dB levels, but the settings were not changed when the circuits were changed, so that the comparisons were "apples-to-apples".

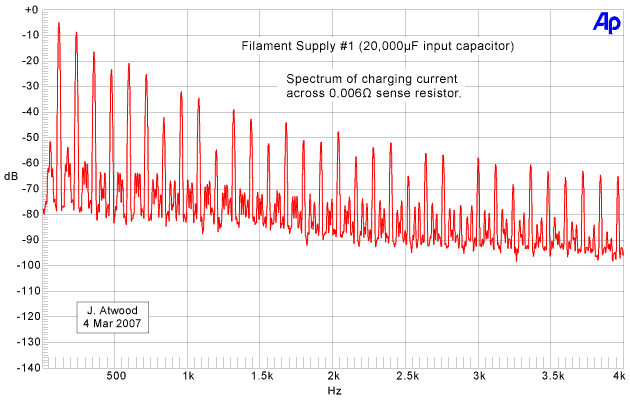
First, let's look at circuit #1. As expected, both the charging current and ripple voltage have significant high-order harmonics. One minor note: if the line current rather than charging current would have been measured, the even-order terms would have been a bit larger.

The harmonics on the charging current are only about -55dB down at 3KHz, compared to the 120Hz fundamental:

For the ripple voltage, the harmonics are about -65dB down at 3KHz:

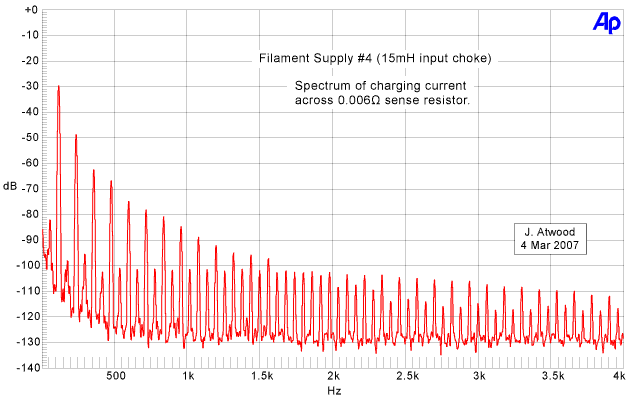
Now, let's look at the choke input circuit #4. First of all, the 120Hz charging current fundamental is -25dB below the cap-input case, and the high-order harmonics fall off a lot faster. At 3KHz, the harmonics are -75dB down from the 120Hz fundamental:

For the ripple voltage, the drop-off is even faster:

Even the "noise floor" between the 60 and 120Hz harmonics is lower in the choke input case. Circuit #3 would have a charging current spectrum similar to circuit #1, but a ripple voltage spectrum just slightly worse than circuit #4.

Update (23 March 2007): A ClariSonus reader requested more FFT plots, especially of circuit #3. I re-constituted the circuit and took FFT plots using the same settings as above. Here are the plots of current and ripple voltage for circuit #3:
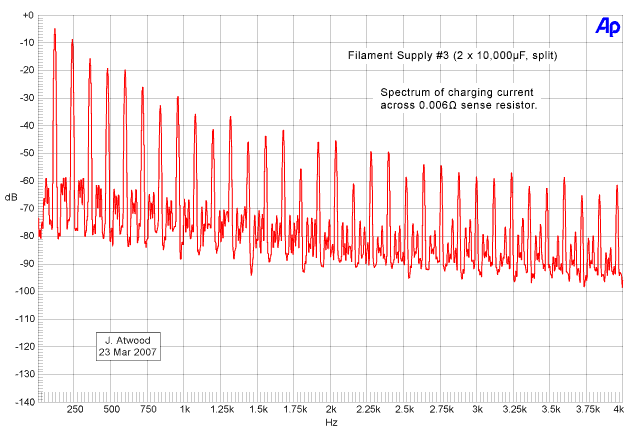
Circuit #3 current

As predicted above, the charging current is similar to circuit #1 and the voltage ripple is similar to circuit #4. However, close comparison shows the following differences:

The low-order current harmonics are almost the same.
The high-order current harmonics are very slightly higher.
The ripple voltage harmonics and noise floor are 10 to 20dB higher than in circuit #4, but 15 to 25dB better than circuit #1.

At the request of a reader, Schottky rectifiers were tried in place of the conventional silicon bridge rectifier. The rectifiers used were General Semiconductor brand MBR-1045 rectifiers rated at 10A and 45V. They are in a two-lead TO-220 package and four were wired in a bridge. They were substituted into circuit #3 and identical FFT plots were made as above. Here are the current and ripple voltage waveforms:
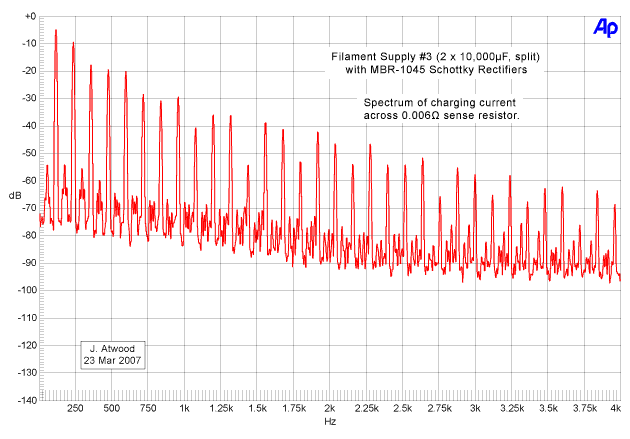
Circuit #3 current w/Schottky

The lower voltage of the Schottky rectifiers resulted in a 0.3 volt increase in output voltage. To compensate, the rheostat was increased to 2.8 ohms to keep the output at 5.0 volts. The results were quite similar, but on close inspection the following can be noticed:

The charging current is virtually identical, except above the 22nd harmonic, where it is lower.
The ripple voltage low order harmonics (1st to 3rd) are about 2 to 4 dB lower.
The ripple voltage medium order harmonics are just slightly higher.
Very high order voltage harmonics (over the 22nd) are noticeably lower.

The reduction in ripple voltage may be caused, in part, by the slightly higher rheostat setting. The main difference seems to be above 2.5KHz, where the harmonics are less with the Schottky rectifiers. The advantage of high speed rectifiers, such as Schottkys, is mainly apparent at high frequencies, where the reduction of glitches caused by stored charge are reduced. This test isn't really set up to measure this, although it becomes noticeable above 2.5KHz. Another set of tests needs to be run focusing on the higher audio frequencies up into the RF domain to compare rectifiers.

Conclusion

The ubiquitous capacitor-input filter is really quite noisy, and almost always requires additional filtering or regulation to eliminate ripple. However, the noisy current draw pollutes everything upstream from the rectifier, and can easily get into other circuits. Adding series resistance helps reduce the charging current, but doesn't help the voltage ripple. Even just a little bit of RC filtering drastically reduces the ripple. A choke-input supply makes both the current and voltage ripple very small. In addition, its quick drop-off of harmonics means that any leakage into signal circuits is not as noticeable, since, due to the Fletcher-Munson curve, the ear is less sensitive to low-frequency noise. If the lack of voltage regulation with load current can be tolerated then circuits #3 and #4 could drive DHT filaments directly. Circuits #1 or #2 would require additional filtering to keep the audible noise down.